Un générateur artisanal de nombres (pas vraiment) aléatoires (PRNG) en Javascript

Il y a très longtemps de ça j’avais développé un petit générateur de nombres « aléatoires » (pseudo random numbers generator) en Javascript pour un projet de jeu, l’objectif étant d’en avoir un basé sur une seed (c’est à dire que donné le même paramètre source il générera toujours la même série de nombres), et qui permette de déterminer un résultat à partir de cette clef et d’un numéro de tirage, sans avoir à générer toute la série de tirages précédents.

Le pourquoi de la chose

En développement ludique, utiliser un PRNG dont on puisse contrôler la clef/seed a beaucoup d’intérêts.
Par exemple, plutôt que d’avoir à sauvegarder toutes les données d’un univers procéduralement généré, on peut le régénérer à partir de la même série de tirages en n’ayant à enregistrer que la seed qui l’a produite.
On peut même aller jusqu’à complètement remplacer un système de sauvegarde classique par une combinaison de random seed et d’enregistrement des actions des joueurs (et en s’offrant en plus le luxe de pouvoir restaurer une partie à n’importe quel stade passé à partir d’un seul enregistrement).
Et avec la possibilité d’obtenir directement le résultat correspondant à un numéro de tirage, sans avoir à calculer toute la série précédente, c’est encore plus pratique.
Imaginons par exemple un PNJ de jeu de rôles ayant de nombreuses caractéristiques déterminées par des tirages aléatoires. Au lieu d’avoir à effectuer ceux ci à sa création et à stocker les résultats, même alors qu’il n’en est pas encore à utiliser ces caractéristiques, on peut plutôt stocker simplement le numéro de son premier tirage, et ne calculer les caractéristiques qui en découlent que si besoin, une série de tirages commençant par un numéro x basé sur la seed donnant toujours le même résultat, il suffit de savoir que la force du PNJ correspondra au tirage (premier tirage +3) par exemple, et le jour où on en a besoin on peut la générer en n’ayant à stocker que le numéro où commencent les tirages qui seront utilisés pour ce PNJ.
Enfin on peut utiliser la prévisibilité des tirages pour simuler des choses comme des pouvoirs de divination, ou encore pour permettre à un adversaire-IA de compenser sa naturelle stupidité en lui donnant le pouvoir de décider de ses actions en connaissance des jets de dés qu’il va faire.
Je reviendrai sans doute sur tout ça dans des messages suivants, mon projet étant de faire du générateur de nombres dont je vais vous parler aujourd’hui la première partie d’un fil rouge que je vais proposer ici, consacré à la programmation destinée au jeu, que je compte pousser jusqu’à la création d’un petit jeu de stratégie en javascript (ou d’aventure ? de management ? un JdR ? Pas encore décidé en fait..), si je trouve le temps.

Quoi qu’il en soit ce sont des choses que ne proposent pas la méthode Math.random() native de javascript (bien qu’elle ne soit pas plus réellement aléatoire : telle qu’implémentée par les navigateurs actuels elle fait appel à un pseudo random number generator nommé xorshift 128+, lui même basé sur un système de seed, si javascript n’offre pas l’option de renseigner sa clef soi même) ; quant à la fonctionnalité moins connue Crypto.getRandomValues() visant à être assez sécurisée pour être utilisée en cryptographie elle apparaît un peu lourde pour de la simple génération de tirages « aléatoires » destinée au jeu (et ne permet pas plus que Math.random() d’obtenir directement un résultat à partir de sa clef et d’un numéro de tirage), de même que la plupart des diverses librairies Js destinées à améliorer la génération de nombres aléatoires (la plus connue étant seedrandom).

Un système inspiré des jets de « dé 100 » dans les Jeux de Rôles sur table

Pour en revenir au petit PRNG que j’avais développé il y a sept ou huit ans, m’inspirant de l’usage des dés à 10 faces pour produire un « dé 100 » dans les jeux de rôles, je l’avais basé sur un nombre assemblé à partir de 3 chiffres. A l’aide de leurs numéros en UTF16 je convertissais les caractères d’un mot en une table de 30 chiffres de 0 à 9, puis avec diverses opérations mathématiques un numéro de tirage en références à cette tableau d’où j’allais extraire centaines, dizaines et unités du nombre à générer.
Au final , j’étais abouti à un système me semblant à vue de nez satisfaisant, sans avoir à utiliser de fonctions de cryptographie ou calculs complexes. Du moins à ce qu’il me semblait après l’avoir testé sur quelques centaines de tirages de dés à 100 ou 1000 faces, parvenant à générer des nombres d’apparence aussi aléatoires que ceux que produit Math.random() mais découlant d’une seed et pouvant être retrouvés à partir de la clef de celle ci et de leur numéro de tirage.

Les tests de ma première version

Puis, ayant abandonné le projet de jeu où je comptais l’utiliser, je n’y avais plus pensé pendant des années,  jusqu’à ce que, cherchant un petit exercice à faire pour pratiquer mon javascript entre deux projets plus sérieux, il me vienne l’idée de retravailler ce code pour le mettre au propre et le rendre public sur Github.
Avant de me ridiculiser, je me suis dit autant faire quelques tests un peu plus poussés, et ai développé une procédure pour vérifier que certains nombres n’étaient pas sur-représentés dans les résultats, ou qu’il n’y avait pas de répétitions fréquentes de même séries de nombres.
Sur quelques centaines de tirages ils semblaient satisfaisants…

Mais sur beaucoup plus, un peu moins…

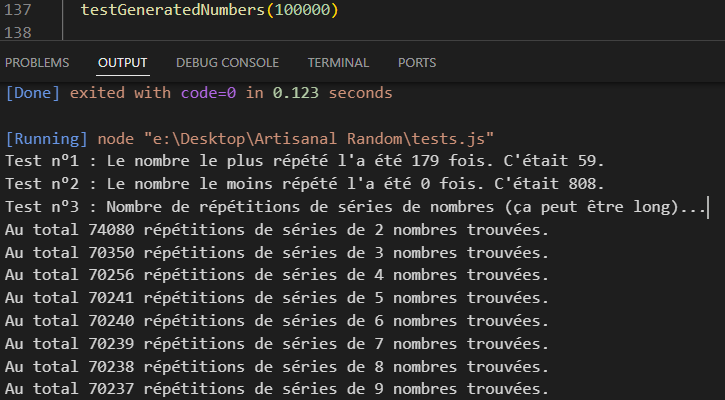
Non seulement ma méthode entraînait un nombre incroyable de répétitions de mêmes séries, mais elle ne générait juste jamais certains nombres.
Elle me semblait pourtant parfaitement logique, ramener le n° de tirage à une valeur de 0 à 29 (30 revenant à 0, 31 à 1, etc.), pour sélectionner le premier chiffre, puis pour les suivants, toujours en ramenant tout à une échelle 0-29, appliquer un décalage basé sur (n° de tirages +1) divisé par 30 (donc pour le tirage 0 les chiffres 0, 1 et 2 composaient le nombre final etc. tandis que pour le 30 ça devenait 0, 2 et 4,  pour le 33, 3, 5 et 7 etc.), et enfin pour les numéros de tirages élevés y ajouter un décalage global de 1 tous les 900 tirages. Ce à quoi j’ajoutais pour plus d’irrégularité un changement de l’ordre des dés si le n° de tirage était un multiple de 2 ou 3. Mon maigre talent mathématique m’aurait fait imaginer qu’elle ne se mettrait à répéter les mêmes séries de nombres qu’au bout de 810,000 tirages environ (900 au carré), quand en fait elle commençait à tourner complètement en boucle dès 27,000 (et présentait de grosses anomalies au niveau de la fréquence des nombres dès bien bien avant).

Le développement d’une seconde méthode

Ne m’avouant pas vaincu, profitant des tests déjà réalisés, j’ai créé une nouvelle version appelée « roll1 » (la précédente devenant roll0), faisant en sorte que les numéros des dés n°2 et 3 ne soient plus en relation directe avec celui du premier (ce qui est ce qui entraînait la mauvaise distribution des nombres), et ajoutant toutes sortes de conditions pour casser les répétitions de séries (du type si le numéro de tirage est un multiple de x le décaler arbitrairement d’une certaine valeur).
A un certain stade, j’ai réalisé que baser des décalages sur les multiples de 30 était juste une mauvaise idée contribuant à multiplier les répétitions de séries, et que pour rendre les nombres générés les plus irréguliers possible il convenait plutôt d’utiliser des formules basées sur des multiplications par des constantes mathématiques ou des fractions complexes (obtenues en divisant un nombre premier par un autre, quitte à ce que le choix de ceux ci soit complètement arbitraire).
Dans cette seconde version l’index du dé numéro 2 par exemple est calculé à partir du numéro de tirage (déjà arbitrairement ajusté par divers facteurs et une constante générée à partir de la seed) divisé par 47 et multiplié par 17 tandis que celui du premier est basé sur ce numéro de tirage ajusté multiplié par Math.PI et divisé par 4 (le tout finissant évidemment ramené au final à un nombre de 0 à 29). Bien que le choix de ces formules particulières ne réponde à aucune logique (et peut être justement pour ça), cela permet d’obtenir des résultats bien plus proches de l’aléatoire qu’avec ma formule originale bien plus carrée.
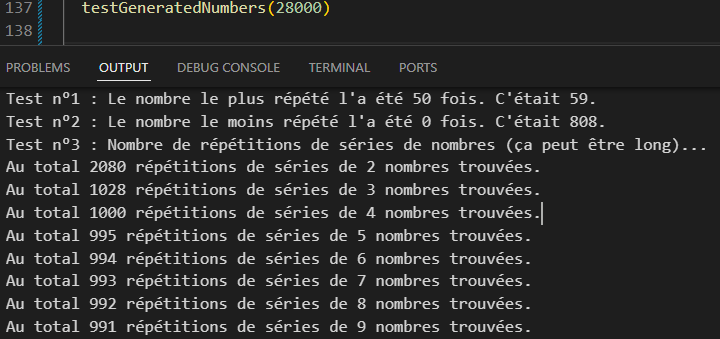
Améliorant peu à peu l’efficacité du tout de test en test je suis finalement arrivé à une répétition de nombres et un nombre de répétitions de séries bien plus raisonnable.

Néanmoins elle restait largement au dessus de la fréquence des répétitions de séries de Math.random(), qui soumise aux mêmes tests, produit rarement plus d’une douzaine de séries de 2 nombres (et généralement aucune de 3) sur une séquence de 100,000 tirages, et le tout tout en étant basée sur un code particulièrement indigeste (une longue succession de if appliquant telle ou telle modification arbitraire selon telle ou telle condition ne l’étant pas moins). De plus à un certain stade, j’avais beau en ajouter je n’arrivais pas à diminuer sensiblement d’avantage le nombre de répétitions.

Une troisième basée sur des calculs aboutissant à beaucoup de décimales…

Ayant réalisé l’intérêt des multiplications par des fractions complexes j’ai alors développé une troisième méthode, roll2, les utilisant différemment : au lieu d’arrondir le numéro de tirage multiplié par elles et de le ramener directement à une base 30, elle convertit le résultat en string, en extrait les 4 derniers chiffres (de nombres en ayant typiquement un paquet après la virgule), les reconvertit en nombre, puis seulement ensuite ramène ce nombre à du 0 à 29 pour le faire correspondre à un dé.
Ce genre de méthode, plus proche de celles qu’utilisent la plupart des PRNG serait même utilisable sans le passage par la table de dés (en utilisant juste les 4 chiffres obtenus), c’est parce qu’on souhaite un résultat basé sur une seed qu’on la conserve.
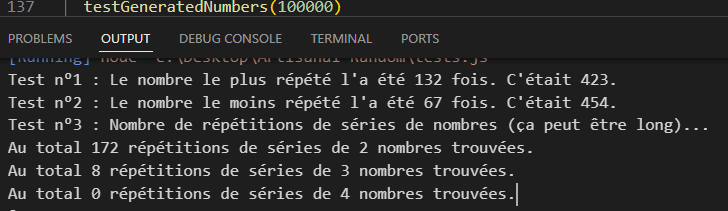
Lors des premiers tests, elle s’avéra néanmoins moins satisfaisante qu’attendu : alors que cela diminuait bien un peu le nombre de répétitions de séries, faisant disparaître celles de 3 nombres, elle aboutissait étrangement à une fréquence anormalement élevée de certains (de l’ordre de plus de 250 apparitions d’un même sur 100,000 tirages, ce qui est une grosse anomalie statistique) et mécaniquement à une sous-représentation d’autres.
Après une série de modifications et de tests, j’ai réalisé (sans même vraiment comprendre pourquoi le garder entraînait ce résultat) qu’éliminer le tout dernier chiffre de mes nombres issus de fractions était ce qu’il convenait de faire pour éviter cette anomalie. Et finalement en passant d’un slice (-4) appliqué à mes résultats de calculs improbables convertis en string, à un slice (-1,-5) je suis enfin abouti à une méthode produisant quasiment un aussi faible nombre de répétitions sur 100,000 tirages qu’un usage de Math.random(), tout en ayant une répartition équilibrée des nombres générés.

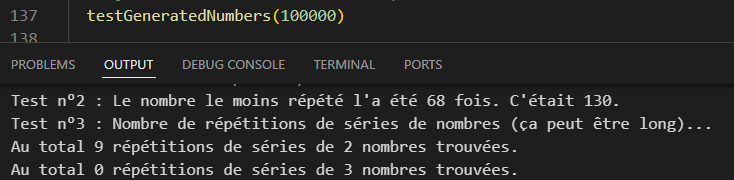
Mais testée sur un encore plus grand nombre de tirages elle se met à partir de 250,000 environ à produire plus de répétitions de séries que Math.random(), si elle reste loin en dessous du nombre obtenu avec la méthode roll1.

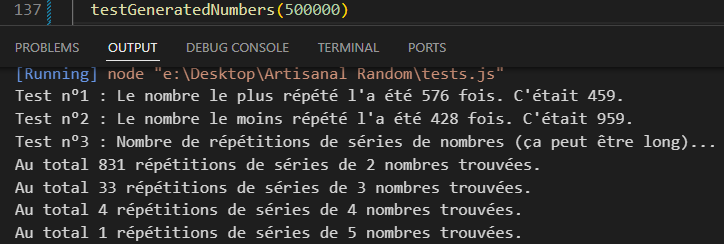
Une quatrième avec plus de variations dans ces calculs

L’idée d’ajouter des variations à mes fractions (en faisant passer mes diviseurs par un cycle utilisant ma fonction rebaseNumber pour le ramener à des limites différentes pour chaque numéro de dé) m’étant venue entre temps, j’ai finalement développé une nouvelle variante, roll3, qui résout ce problème (produisant moins de répétions de séries de nombres que Math.random() en moyenne, au moins jusqu’à 500,000 tirages).

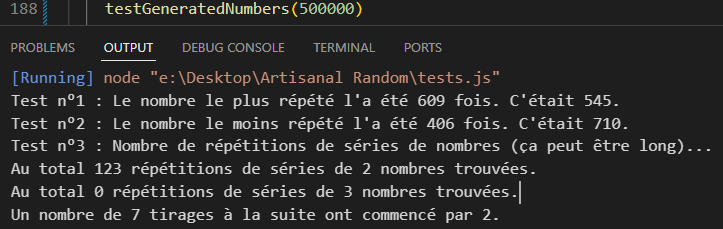
(Math.random() soumis au même test donne 125 répétitions de séries de 2 nombres en moyenne, et assez régulièrement une poignée de séries de 3 ou de 4.)

Elle n’est ceci dit pas parfaite, étant nettement plus lente à exécuter (si elle reste plus rapide que Crypto.getRandomValues(), l’autre option de PRNG offerte nativement par javascript). Mais comme on parle en nano-secondes de toutes manières, c’est sans grande importance, je ne vois pas trop de contextes où on aurait besoin d’effectuer un million de tirages en moins des 2 secondes que ça lui prend.
Et par ailleurs elle ne permet pas d’effectuer des tirages à plus de 1000 possibilités (si ce n’est pas dur à développer avec la même approche, il suffit d’ajouter des « dés » aux indexs choisis en utilisant le même genre de formules – j’ai d’ailleurs fini par le faire dans une nouvelle méthode, rollLarge, permettant de tirer jusqu’à des dés allant jusqu’à 1 milliard de faces, que je ne détaillerai pas ici, mais est incluse dans le code à télécharger).

Un succès attribuable à une approche basée sur les tests

Mais si j’écris tout ça, c’est moins pour me féliciter de ce succès que pour insister sur ce qui m’a permis d’y arriver, à savoir ce qu’on appelle une approche Test Driven, déterminer d’abord le résultat qu’on veut obtenir (ici une méthode aboutissant à une répartition des nombres équilibrée et aussi peu de répétition de séries que possible sur un grand nombre de tirages), établir une batterie de tests nécessaires à vérifier qu’on s’en approche, puis ajuster son programme ou essayer de nouvelles approches jusqu’à les satisfaire.
Comme on l’aura compris je suis tout sauf un spécialiste des probabilités et plus encore des formules mathématiques permettant de créer l’illusion de l’aléatoire. Sans les tests j’aurais été totalement incapable même de voir que ma solution originelle était erronée. Ce n’est que par une succession d’essais, d’erreurs et de … d’avantage de tests que je suis finalement arrivé à un résultat satisfaisant.

A noter par contre que si je parle d’approche Test Driven, je n’ai pas pour autant utilisé un cycle de Test Driven Development dans sa version la plus académique / formelle, qui se baserait plutôt sur la recherche d’un résultat très précis (assertion à satisfaire), et la rédaction de tests unitaires (d’une seule fonction à la fois, isolée de son environnement, les données qu’il lui fournirait en temps normal étant remplacées par des valeurs de test) à passe et retournant une valeur booléenne (soit la fonction a complètement réussi à aboutir au résultat voulu soit échoué), le tout envisagés l’un après l’autre (en ne passant à la rédaction d’un second test qu’après avoir passé le premier etc.).
Ce que j’utilise plutôt ici c’est des tests de performance (et/ou d’acceptation si on considère les résultats que je cherche à obtenir comme répondant à une « exigence métier ») : un très grand nombre d’exécutions répétées de mes fonctions dans leur environnement naturel, pour en tirer des données statistiques sur leur fiabilité, et chercher ensuite à l’améliorer (ici aboutir à une répartition des tirages plus équilibrée, et le moins possible de répétitions de séries de nombres), sans qu’il y ait à proprement parler de possibilité de réussite ou échec total de ces tests (enfin à part les maintes fois où une faute de frappe dans un nom de variable ou un calcul aboutissant à une division par 0 faisait tout planter ;).
Évidemment si une modification de mes formules conduit à une augmentation du nombre de répétitions lors de ses tests au lieu de le réduire par rapport à la version précédente, je la traite comme ayant échoué, mais sans avoir jamais précisé le résultat exact auquel elle était censée aboutir.

On pourrait en fait également assimiler cette méthode à ce qu’on appelle du Data-Driven Development, mes tests pouvant être vus comme des moyens de collecte de données plus que des tests à proprement parler (du fait qu’ils ne contiennent aucune assertion ou condition de réussite, ne faisant que fournir des données à utilité statistique), et mes choix découlant de celles ci.
D’un autre coté ce qu’on entend généralement par DDD, c’est plutôt de la collecte de données du style retours d’utilisateurs d’un programme, pas de simples résultats d’exécution, suivie de leur examen par des outils d’analyse statistique ad-hocs (typiquement écrits dans des langages orientés analyse data comme Python), pas de simples comparaisons. Je ne suis donc pas non plus dans une application formelle de ses méthodologies.

Quoi qu’il en soit la classification de celle employée est bien moins importante que l’idée générale d’axer un développement sur des tests (ou des collectes de données selon comment on préfère les appeler).

Les principales fonctions du générateur en détail…

rebaseNumber

Fonction essentielle à toutes les autres, rebaseNumber celle qui permet de convertir un plus grand chiffre (ou éventuellement un plus petit) en valeur de 0 à 29 (ou toute autre limite spécifiée, mais je lui donne un défaut de 30 car c’est celle que j’utiliserai le plus).
Elle consiste simplement, après s’être assuré que le paramètre number soit un nombre entier, à lui retirer une valeur égale au nombre de fois il est divisible par la limite, multiplié par elle. Ainsi par exemple 300 se verra retirer 30×10 et sera ramené à la valeur 0.
Dans le cas d’un nombre négatif, on le multiplierait simplement par -1 et ferait de même (si en pratique ce n’est pas utilisé, les versions actuelles de WordToSeed et roll3 ne transmettant normalement à cette fonction que des nombres positifs).

wordToSeed

wordToSeed est la fonction permettant d’utiliser une chaîne de caractères comme clef.
Elle commence par vérifier qu’une chaîne lui a bien été soumise en argument. Si ce n’est pas le cas elle ne retourne rien (ce qui entraîne l’utilisation d’une autre méthode de génération de la seed à l’initialisation de RandomSeed), sinon elle initialise un tableau de 30 nombres, prenant au départ la valeur -1.
Comme on veut que cette chaîne fasse au moins 30 caractères, on commence par l’allonger si elle est plus courte, en la répétant jusqu’à ce qu’elle fasse cette longueur.
Quelques caractères (arbitrairement choisis) sont également ajoutés à chaque répétition, pour éviter une clef qui ne soit que la répétition en boucle d’un ou deux (ce qui rendait trop régulière la suite de chiffres obtenue, ce que les tests ont montré avoir un impact sur les répétitions de résultats).
Ensuite on converti les lettres une à une en nombres à l’aide de l’instruction charCodeAt retournant leur code utf-16 sous forme d’un entier.
Ces nombres sont transformés en valeur de 0 à 29 et servent à placer chaque chiffre (correspondant aux unités de l’itérateur de la boucle permettant de parcourir la chaîne de caractère) dans la case correspondante du tableau si elle est libre (sa valeur égale à -1).
Si elle est déjà occupée par un chiffre, on décale le placement du nouveau (soit en avant soit en arrière) jusqu’à tomber sur une case libre.
Et enfin, une fois toutes les cases remplies on retourne ce tableau.

RandomSeed

RandomSeed est l’objet qui stockera cette table, ainsi que le numéro de tirage depuis que le programme a été lancé, et une valeur constante à lui ajouter pour les différents calculs.
Si aucune seed (table de chiffres) ne lui est fournie elle appelle une autre fonction, genSeed (que je ne détaillerai pas ici, mais qui marche globalement comme WordToSeed à part qu’elle se base sur des tirages aléatoires plutôt que des codes de caractères) pour en générer une.
Elle initialise également le numéro de tirage à 0 s’il ne lui est pas fourni.
Enfin si elle n’est pas fournie, elle génère la valeur addToRollNo, en assemblant ‘10’ et un certain nombre de chiffres arbitrairement choisis de la table pour aboutir à un nombre à 7 chiffres.
L’importance de cette constante est une des choses découvertes lors des tests. Utiliser un nombre trop court, ou un qui ne commence pas par 10, a tendance à entraîner d’avantage de répétitions de séries lors des résultats finaux (ne me demandez pas d’expliquer exactement pourquoi, comme déjà dit je ne suis pas mathématicien), tandis qu’un plus long ne les réduit pas (probablement car on ne garde que quelques chiffres des calculs faits avec).
Si on ne voulait que générer des nombres « aléatoires », elle aurait pu être directement ajoutée à rollNo puisque c’est systématiquement fait dans les méthodes « roll », mais comme on veut aussi pouvoir retrouver un résultat à partir de sa clef et d’un numéro de tirage, on préfère conserver ce nombre à y ajouter à part.

RandomSeed.roll3 (la plus efficace de mes méthodes de tirage de nombres)

Comme les autres elle commence par vérifier si on lui a fourni un numéro de tirage, et si ce n’est pas le cas utilise et incrémente celui de sa RandomSeed (sinon, au cas où le paramètre fourni soit sous forme de string par exemple, elle s’assure qu’il soit converti en nombre entier). Ensuite elle ajoute à ce nombre la constante évoquée plus haut.
Puis elle détermine 3 diviseurs qui vont servir aux calculs utilisés pour les 3 chiffres, en convertissant pour chacun le numéro de tirage en valeurs de limites différentes, et ajoutées à des constantes différentes.
C’est son principal ajout par rapport à ma méthode précédente, roll2 (qui utilisait elle des diviseurs fixes), et ce qui lui évite de répéter autant de séries de nombres même après un très grand nombre de tirages.
Le numéro de tirage, multiplié par une valeur arbitraire (soit la constante Math.PI soit un nombre premier), est ensuite divisé par ces nombres, et jusqu’aux 5 derniers chiffres du résultat obtenu moins le tout dernier, déterminent le nombre à ramener à une valeur de 0 à 29 pour sélectionner les case de la table seed à utiliser. C’est là encore les tests qui ont conduit au choix de ne pas garder le tout dernier chiffre, ou d’en utiliser 4 plutôt qu’un autre nombre.
Entre temps on opère à des inversions de l’ordre des dés si le n° de tirage est multiple de 3, ou de 2 sans être multiple de 3 (là encore c’est arbitraire, mais efficace au niveau des tests pour réduire le nombre de répétitions de séries).
Le résultat final est alors assemblé sous forme d’une valeur de 0 à 999, et si le numéro de tirage est un multiple de 4 cette valeur est inversée (devenant 999 – elle), une autre opération le réduisant.
Enfin si un dé a été spécifié la valeur est ramenée à un nombre approprié, comme on convertirait un pourcentage, et on retourne le résultat (augmenté de 1 comme il est plus fréquent de vouloir utiliser des tirages de dés allant de 1 à leur borne supérieure comme dans le monde réel, plutôt que de 0 à cette borne supérieure -1).
Et pour utiliser tout ça il n’y a plus qu’à employer :

Avec en paramètres optionnels une valeur maximum de dé (inférieure à 1000 si on veut que toutes les valeurs entre 1 et celle ci puissent apparaître), et le numéro de tirage à utiliser.

Vous pouvez retrouver les tests utilisés et autres méthodes sur ma page github consacrée ou en téléchargeant ce code d’ici.

ps : La suite du projet de Jeu Fil Rouge. Est par là…